時間の矢

　おそらくＫ中間子はこの世で確認されている唯一の時間反転物質である。これまで、どんな素粒子の反応にも時間の逆転など一度も観測されたことはない。たとえ１００万分の１秒程度の出来事ではあっても、原子核反応のすべての現象で時間の対称性は守られていた。多くの原子核は電子を放出するとたちまちベータ崩壊して反粒子をつくるけれど、そこでも時間はちゃんと流れていた。それがＫ中間子だけには時間の反転が見られた。なんということか。
　このことを知ったときは驚いた。何かがこみあげてきて、ちょっと嬉しかった。この嬉しさは、パストゥールが酒石酸の旋光現象における左旋性に注目して「私たちが目にする生命は宇宙の非対称性の結果である」と言ったことを知ったときとか、コバルト６０のベータ崩壊でパリティ対称性が破れたことを知ったときの嬉しさに似ている。ふっふっふという嬉しさだ。
　もっともＫ中間子は人工的にしか観察されたことがない。自然界にあるとは断定できない。加速器の中で見えるだけである。それも３種類のＫ中間子があって、１つはプラスの電荷、１つはマイナスの電荷、１つは中性になっている。このうちの中性Ｋ中間子だけがごくわずかではあるけれど、時間の対称性を破ってしまうのだ。
　これで充分ではないかという気がする。すでに特殊相対性理論は観測者にとっての時間の歩みを伸ばしたり縮ませたりしたのだし、一般相対性理論は時間を単独で扱うことをあきらめさせて、時空連続体という見方をしなければ話にならないというところまであきらかにしたのだ。しかし、話はそうかんたんではなかった。
　
　陽電子が発見されてその研究がすすんだとき、かのファインマンがおもしろいことを仮説した。
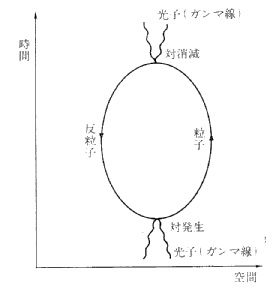
　ほとんどの粒子には反粒子があるのだが、その粒子と反粒子が衝突すると互いに消滅（対消滅）し、その場にエネルギーが発生する。たとえば電子とその反粒子である陽電子がぶつかると、２つが消えてガンマ線が出る。この反応は物質がエネルギーに変換した例で、世界で最も恐ろしい関係式といわれるアインシュタインのE＝mc²から導ける。
　物質がこのようにエネルギーに変換されるのなら、この逆のプロセスもおこるかもしれない。事実、ある状況のもとでガンマ線が粒子と反粒子の対に変換することがある。ガンマ線がある条件のもとではガンマ線自身を消失させて、そこに電子と陽電子がひょっこりあらわれるのだ。
　ファインマンはこのことを、陽電子が「時間を逆向きに動く電子」になったというふうにみなしてもかまわないのではないかと仮説した。これはおもしろかった。何事にも出現と消滅があるけれど、電子においては突然の時間の逆転が消滅なのである。時間の物理学についてはときどきこういう発想が出てくるから、ふっふっふなのである。

ファインマン図
反粒子には未来から過去の方向に矢印がついている

　ファインマンの仮説はまだ証明されていない。しかし、このようなことが時間をめぐって許容されているというのは、時間そのものを相手にした議論としては、もう充分なほどの思考実験をしてきたことを告げているように思う。
　たとえばブラックホールでは、時間が重力場の外に出ることすらできないと考えられている。そこにはシュワルツシルトの半径という、この世で一番厳格な半径ががんばっている。むろん証明されたわけではない。しかし、時間なんてそんなものではないかと思うのだ。ホーキングはいっとき、ブラックホールが少ないほうが「過去」で、ブラックホールがふえていくほうが「未来」だと考えたほうがわかりやすいんじゃないかと言ったほどだった。大半の科学が扱う時間に対称性が成り立っているからといって、科学が時間の不可逆性にしがみついていることはないのである。ぼくは漠然とそう感じている。
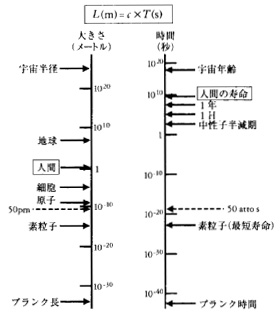
　おそらく健全な科学では、時間というものは有史以来、特定の方向に向かって一様に流れているもので、宇宙がビッグバンこのかた膨張していることに由来するというふうに解釈するのだろうけれど、だからといってそれがどんな細部の現象にもあてはまると考えるのは、堅すぎる。そればかりか、生命にとっての時間や情報にとっての時間を考えると、Ｋ中間子で時間の対称性が破れたくらいのことは、とっくにおこっているとさえ言いたくなる。ようするに、時間をひとつの線的な現象として扱うのは、そろそろ限界にきているということなのである。

宇宙の時間軸と空間軸での人間の位置づけ

　時間を考えるのは好きだ。時間に関する書物もおおむねおもしろい。どのくらい読んできたかわからないが、きっと１００冊をこえているだろう。本気で時間の正体を究めたいと思って読んだのではない。緑陰でワッフルやパンケーキを紅茶とともにつまむように読んできた。シロップやバターの出来が悪いのもまじっていた。
　インド哲学と蓮の研究で名高い松山俊太郎さんは「時間については５００冊は読んだねえ」と豪語したあとに、「ところがね、読めば読むほどとんでもないことになってくるんだよ」と笑っていた。
　古代インドでは時間は流れない。そういうことをあらわす言葉がない。「流れる」ではなくて、「静止」「持続」「消滅」があるだけなのだ。だからインド哲学や仏教の時間論は、経典の文中に「静止」「持続」「消滅」の同義語や反意語があるたびに言及されているといっていい。わかりやすいところでいうなら、たとえば「色即是空」という言説ですら時間論なのである。松山さんのようなインド哲学者が５００冊の時間論を読んだとしても不思議はなかったのだ。
　ぼくのばあいはどうだったかというと、最初に道元の「有時」をめぐる発議やアンリ・ベルクソンの瞬間と持続を対比させた時間論に色気を感じたのがよかったのか、そうではなかったのか、いまとなってはわからない。また、そのころ国際時間学会の会長をしていたジェラルド・ウィットロウの『時間 その性質』（法政大学出版局）や渡辺慧の『時』（河出書房新社）を当初に読んだのが薬効なかったのか、そうでもなかったのかも、判定しがたい。時間ワッフルなら手当たりしだいにむしゃむしゃやってきたぼくの嗜好がそもそも奈辺にあったのかは、いまや時の彼方の出来事の影響というしかないわけだ。
　
　古代人は総じて、時間を循環的なもの、周期的なもの、もしくは円環的なものだと想定していた。また、古代ギリシアにおけるアイオーンやカイロスやクロノスのように、時間といっても民族や地域によってはいくつも種類があった。「永遠」と「瞬間」は異なる時間なのである。サンスクリット語のカーラは時輪と訳せるけれど、あれは時間をバームクーヘンのように重ねて眺められるようにしたものだ。時間は好きに選んだり、積み上げたりできたはずなのだ。
　それがだんだん直線的な時間の観念ばかりが大手をふるようになっていったのは、おそらくユダヤ・キリスト教のせいである。とくにキリスト教が天地創造を特定時点での開始とみなしたのに辻褄をあわせて終末論というものをもちこんでから、時間はせっせせっせと直線を流れるようになった。時間は不分明な開始と忌まわしい終点をもったのだ。いまでは紙の上に鉛筆で左から右に向かってさっと１本の線を引き、そこに任意の一点を打って、「ここを現在とするとね」といえば、誰もが左は「過去」で、右が「未来」というふうに認識するようになってしまった。かつてインド仏教では「三世実有」とも「過未無体」とも言ったのに……。

　科学において、キリスト教的な時間の流れの見方に乗ったのはアイザック・ニュートンである。ニュートンは絶対空間とともに絶対時間を確定し、ｔと-ｔ（マイナスｔ）とのあいだの不可逆を樹立してみせた。
　これはその後の科学と哲学の大半をのせる土台になっていく。世の家系図もダーウィンの進化論もこの「時間の矢」の絶対進行を疑わない。世の中の見方も、脱進機のついた機械時計の普及とともにこの矢を疑わなくなった。世界はたった１種類の時間の支配下に入ったのだ。
　言い忘れないうちに書いておけば、このことに哲学的反旗をひるがえしたのがニーチェだった。ニーチェの「永遠回帰」の思想とは、キリスト教的な「時間の矢」に対決するためのものだったといってよい。ニーチェには古代ディオニソスの循環時間世界が蘇
っていた。しかしこれはあまりに遅すぎた。すでに１９世紀の後半は、直線的な時間の流れに乗って近代科学の基礎の大半が築かれていた。
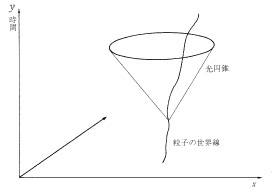
　もうひとつ言い忘れないうちに書いておけば、こと時間の科学や哲学に関するかぎりは、ニーチェは線状的なキリスト教型時間を壊すためにわざわざ永劫の循環時間をもちだす必要などなかったのである。いまでは時間の科学は「時空図」というＸ軸に空間をＹ軸に時間をあらわしたグラフ上にあらわすようになっていて、そこでは「過去」も「現在」も「未来」も同時に存在しうるようになっているからだ。これはアインシュタインの相対性理論を理解するにはどうしても手放せない。

時空図の例
光の進む道筋が光円錐とよばれる

　物理学の法則の大半は微分方程式になっている。微分方程式がわからないではフィジカル・イメージはほとんど描像を結べない。これは科学が扱う物理量の大部分が時間とともに変化しているからで、そのために微分方程式がある。またそのため、科学は「時間とともに変化するものとは何か」をめぐっていくつかの劇的な結節点を迎えた。そして、その結節点のつど、奇妙な時間のふるまいとの闘いが何度も演じられた。
　最初の結節点はおそらく数学が「瞬間」や「極限」や「無限小」に立ち向かったときで、これはニュートンやライプニッツが微積分の方法を発見（発明？）して、「限りなく微小な不可分割量」や「生成しはじめる増分」という考え方を白日のもとに引きずり出したせいだった。どんなすぐれた科学もそうであろうけれど、この考え方も当初はかなり分の悪いものだった。知覚の相対性に関心をよせた１８世紀初頭の怪僧ジョージ・バークリー（ぼくがいっときハマった『人知原理論』岩波文庫の著者）は、無限小だなんてまるで「死んだ量の幽霊」のようなものじゃないかと揶揄したし、ニュートン力学のフランスへの普及に貢献したはずのヴォルテールでさえ、微積分は「存在さえ考えられないものを厳密にしようとしている技術」だと冷笑した。
　しかし、やがて微積分法と微分方程式こそが自然界の摂理を牛耳っているだろうことがあきらかになっていった。いわゆる「ラプラスの魔」の存在だって、微分方程式の全能ぶりに惚れての発案だった。ラプラスは、自然の運動に関するどこか一点の運動方程式がわかれば、その次の瞬間の運動もその次の瞬間の運動も確定できるのだから、宇宙のどこかにはそうした運動のすべてを知っている全知全能の魔物（決定論の魔物）がいるということを“予言”したわけで、この魔物も微積分法が正当でなければその存在は許されないはずなのである。
　そのうちコーシーが無限小という厄介を「極限」の概念に替え、さらにワイエルシュトラスがこれを洗練させると、微積分法は迷妄まじりの論理の矛盾を払拭したものになった。そのとき、時間が微分方程式に隠された科学の主語として全世界に躍り出たのである。けれどもここまでは、まだしも数学の冒険が先行していたドラマだった。時間をめぐる最も難解な結節点は、まったく意外なところから、熱力学第２法則によってやってきた。

　熱力学第２法則は、「エネルギーを或るかたちから別のかたちに変えるどんなプロセスにおいても、エネルギーの一部は必ず熱となって散逸する」というもので、物理法則のなかではいつも特別扱いされてきて、最も深遠な法則だとみなされてきた。
　熱力学の法則は、他の物理法則にくらべて格段の真相を秘めているものではあるけれど、言明していることは明確で単純である。熱力学第１法則の「エネルギー保存の原理」とともにくだいていえば、第１法則は「無から何かを生み出すことはできない」、第２法則は「その収支の辻褄はあわない」と言明したわけだ。第３６８夜にピーター・アトキンスの巧みな説明があることを紹介しておいた。
　そのくらい紛れもないような法則なのに、では熱力学第２法則はどうして時間の問題に立ちはだかる結節点になったのかといえば、近代科学が地球の起源や宇宙の起源や原子の起源の解明に乗り出したためだった。
　
　ジェームズ・ハットンは１７９５年の『地球の理論』（未訳）で、岩石や鉱物を分析すれば地球は少なくとも数１００万年の時間をへてきたはずだと説いて、「現在というのは過去を含んでいるのだ」という仮説を発表した。斉一説という。これをチャールズ・ライエルが１８３０年に『地質学原理』（朝倉書店）に普遍化して採用し、この『地質学原理』を携えてダーウィンがビーグル号の航海に出て、かの進化論を確立した。地球や地質が時とともに変化してきたのなら、生物もそれに沿って進化してきたと考えたのだ。
　これらはこの世のすべての発展・進化・進歩は時間とともに未来に向かっているという通念を世の中に植え付けた。ハットン、ライエル、ダーウィンは正真正銘の自然科学者ではあったけれど、そこには「時間とともに進歩するものがある」という明白な含意があった。進歩思想とでもいうものだ。それを社会の通念としてハーバート・スペンサーやトマス・ハックスリーが抜き出した。そのため近代社会のいっさいの進歩思想を支えるエンジンが、一挙にまわりはじめたわけである。
　ところが、時間とともにすべてがうまく進むとはかぎらないのではないかという見方が出てきた。それが熱力学第２法則というものだった。このことに最初に気がついたのは、クラウジウスとともに熱力学の法則を導いたケルヴィン卿ことウィリアム・トムソンである。ケルヴィンは世界を斉一的な時間によって解明するのには無理があると考えた。それは効率の悪いこと、辻褄があわないことが時間とともにおきているという警告だったのだ。
　このような熱力学の示唆を社会通念がうけいれるのは容易ではない。いまでも熱力学的な時間のことを理解している社会人なんて、ごくわずかしかいないだろう。
　
　熱力学と時間の関係というのは「エントロピーの矢」をどう考えるかという問題である。「エントロピーの矢」が「時間の矢」や「情報の矢」とどういう関係にあるのかという問題である。
　この問題は全物理学にとっても全生物学にとっても、かなりの難問だ。エントロピーの動向は平衡系と非平衡系ではまったく異なる様相となるし、閉鎖系と開放系でも異なっている。生物は非平衡開放系に属しているのだから、たんなる物理的熱力学的な現象とは区別しなければならない。だから、腰を入れて議論せざるをえない問題だ。
　まだそういう哲人はあまり出現していないけれど、エントロピーと時間の関係は、科学を成立させている根拠を問題にする哲学にも関与する。それゆえ、時間の正体を究めたいのではなく、時間の議論に遊びたいという意向をもつぼくとしては、こういう問題をとりあげるには、今夜のようなワッフル気分をかなぐり捨てて、あらためて姿勢をたださなくてはならなくなってくる。
　それに「エントロピーの矢」がどういうものであるかを理解するには、その前に時間の科学が２０世紀になって未曾有の解釈の変更を迫られていたことを知っておかなくてはならない。このことも時間ワッフルを食べるお気楽な気分のままでは書きにくい。でも、そこにふれないでは「時間の矢」は見えてこないだろうから、少しだけ感想を書いておくことにする。
　
　２０世紀になって、時間の科学はめまぐるしい変転を見せてきた。次から次へと結節点がやってきた。そのため、ほんとうのところは時間の科学は自立できなくなったというほうがいいほどだ。
　たとえば、原子核の物理学を拓いたラザフォードは原子の“生存時間”を問題にしたのだが、やがて量子力学が急速に拡充し、素粒子の相互作用があきらかになるにつれ、時間は極小粒子のふるまいによってあらわされているのではないかという考え方のほうがおもしろくなってきた。「有限」というものを極小に向けて考えようとすれば、その有限をあらわす現象（たとえばベータ崩壊）が時間そのものの発生の出来事に見えてくるからである。
　いまさら説明するまでもないだろうが、アインシュタインが特殊相対性理論で披露した時間のふるまいも驚くべきものだった。特殊相対性理論は、「空間的にへだたった出来事には同時はありえない」という理論で、運動状態の異なる観測者によってなされた時間測定は一致しないということを告げた。ある観測者には「過去」であることが、他の観測者には「未来」になることがありうる。アインシュタインは、はっきりそう言明したのである。
　これを時間のほうからいえば、時間は空間のなかで伸びたり縮んだりしているということになる。また観測者のほうからいえば、運動している観測者にはそれぞれの「固有時」というものがあるということになる。ここに、２０００年にわたって疑いもしなかった「同時」の真実が崩れたのだ。
　このとき、もはや時間を時間としてだけ追いかけることが不可能になったのだった。近代科学による時間の科学はここで立ち往生したのだ。物質が時空の曲率や重力場のシワそのものを意味することになったように、時間は空間とくっつき、分離不能のものになったのだ。ファインマンが陽電子は時間を逆向きに動いていると見たのは、電子の動向の裏側に時間がひっついてしまったということなのである。
　だから２１世紀に純粋な時間の科学だけにとりくみたいということは、あらかた不可能になったと諦めてもよかったのだ。ぼくがあらためて時間論だけを読書の旅から引き出しにくいというのも、このせいだ。むしろ古代に戻って「いくつもの時間」とつきあいなおす気分になったほうがいいくらいなのである。
　とはいえ、２０００年も続いた時間の観念をニーチェのように古代回帰してすませるわけにはいかない。かなりの超難問ではあるが、科学者たちは「いくつもの時間」の分類と縁組を検討するしかなくなった。それがいいかえれば、いったい、「時間の矢は何本あるのか」ということなのである。もうすこし正確にいえば、時間の方向は何をもってどのくらい区別できるのかということである。
　ここで話が戻ってくる。時間の矢の本数を数える段になると、やはり熱力学がもたらす時間、すなわち「エントロピーの矢」が厄介なのだ。この矢は宇宙開闢以来の秘密を握っているからだ。
　
　本書では、時間の方向を区別するには、少なくとも５本の「時間の矢」をもちださなければならないと書いてある。
　第１の矢は「宇宙膨張がもたらした時間の矢」である。これはわかりやすい。宇宙の物質が過去には圧縮し、未来に向かって分散していることをあらわしている。
　第２の矢は「熱力学の矢」で、これが「エントロピーの矢」にあたる。ちょっとだけ気分をただして、あとで少々案内したい。
　第３の矢は「光の矢」で、もうすこし正確にいえば「電磁気学的な矢」ということになる。光を含む電磁波が過去から未来に向かっていることを示す。この矢が少しでも曖昧なそぶりをあらわすなら、過去のどの一点にも信号をおくることが可能になって、ほとんどの因果律が壊れてしまう。タイムマシンもすぐ作れることになる。だからこれが崩れることはめったにないだろう。
　それでも１９４５年のこと、ホイーラーとファインマンはこの矢と宇宙膨張がどこかで関連していることを示唆して、物質がなんらかの理由で時間を“吸収”するという仮説をたてた。おもしろい仮説だったが、いまのところこの見方は証明されてはいない。もし実証されれば、「未来から収束してくる波動」というものを想定することになり、ぼくとしてはまたニヤッとしたくなるのだが……。
　第４の矢は今夜の冒頭に書いたような、たとえばＫ中間子が見せた「人工時空における逆時間の矢」である。このことはもっともっと議論されたほうがよい問題で、Ｋ中間子だけがあらわしたものではないはずだ。ひょっとすると、ここには物質の旋回性や対称性の問題がからまってきて、かなり複雑な様相を呈するはずなのだが、モリスは本書ではまったくふれなかった。
　第５の矢についても、本書は言及していない。ただ「意識の矢」があるだろうと指摘しただけだった。むろんここにも生物時計のありかからセロトニン（神経伝達物質の１つ）の作用まで、ざっと１ダース以上の時間の区別が認められるはずである。
　このほか本書はほとんど話題にしなかったのだが、第五の矢の手前に「生物を成立させている矢」というものが想定されてよく、これは今後の科学が必需品とするだろうと思う。さらにこのあたりの見方を広げていけば、おそらく「情報の矢」というものがあるはずなのである。しかし、この第６、第７の矢を今後に議論するにも、第２の矢にあげた「エントロピーの矢」が掴めなくてはならないわけである。
　
　さきほども書いたように、熱力学第２法則は「エネルギーを或るかたちから別のかたちに変えるどんなプロセスにおいても、エネルギーの一部は必ず熱となって散逸する」ということを言っている。ところが、分子の衝突、原子核の反応、物体の運動、惑星の動向などとは異なって、熱の散逸は時間に対称的ではないプロセスをもつ。
　熱というものはほうっておけば、どんなときも熱い状態から冷たい状態に流れる。自然ではこの逆はおこらない。これがエントロピー増大の法則が示す「エントロピーの矢」のふるまいだ。
　けれども熱が逆向きに流れるということ、熱を逆向きに流すようにすることは、自然の摂理にさからいさえすれば、いくらでもできる。冷蔵庫がそのようになっているのだが、冷蔵庫のモーターは外から電気を入れて熱を汲み出して、これを外部に放出している。これはエネルギーを消費しているということにあたる。物理学の用語ではこれを「仕事をした」という。
　つまりエネルギーを消費して仕事をするようにしさえすれば、熱は逆向きに流れるのである。外部に熱を流し出せるなら（これが「散逸」だ）、「エントロピーの矢」に逆行する出来事をおこしたっていいわけなのだ。
　生命系こそがこのことをやってのけた系だった。生命系は冷蔵庫ではないけれど、太陽と地球がもたらす熱力学的な外部環境（エネルギー）をうまくつかって、情報転写や物質代謝をやってのけるバイオモーターをつくり、これを動かしつづける自律的なしくみをつくった。
　そこではエントロピーを増大させないようなしくみが仕上がった。生命系は、シュレーディンガーが言ったように「負のエントロピー」を食べたのだ。
　エントロピーは事態を無秩序に運ぶ矢をもっている。それなのに生命系はその矢に対抗して秩序をつくる。むろん宇宙全体からみれば太陽―地球では大エントロピーが支配しているのだが（だからいずれは太陽の燃焼か地球の危機とともに生命系をあやしくさせるはずではあるけれど）、少なくとも生命系というものをひとつの“数１０億年のつらなり”と見るのなら、そこでは小エントロピーを吐き出すしくみがみごとに成立したということなのである。そうだとすれば、この小エントロピーの処理の仕方に時間の処理が（したがって情報の処理が）まじっていてもおかしくはない。
　
　エネルギーを消費して仕事をする能力をもつ系のことを、熱力学では「非平衡系」という。熱の散逸を内外のエネルギーの差で処理している系である。エントロピーが増大するばあいは、その系では非平衡が欠如していく。すなわち利用可能なエネルギーが消失していくことが、エントロピーが増大することなのだ。
　エントロピーの増大は閉鎖系でしかおこらない。系として閉じているところにエントロピーの増大がおこる。これは熱力学閉鎖系というものになる。宇宙全体は、当たり前のことではあるけれど、巨大な熱平衡に向かっている閉鎖系である。ここでは大エントロピーが支配する。
　一方、外部の影響をうける系、いいかえれば外部の影響によって仕事ができる系は熱力学的には非平衡な開放系である。宇宙には外部はないから（そう定義したのが宇宙だ）、宇宙全体に開放系を想定することは意味がない。つまり大エントロピー全体の流れには開放系はない。そのかわり宇宙の局所には、小エントロピーとの拮抗をくりかえしているような適度な開放系はいくらでも想定することができる。太陽と地球がつくりあげた系が、この小エントロピーとの拮抗の舞台となった開放系だった。
　こうして、すべての地球上の生命がこの非平衡開放系をたくみに活用した「負のエントロピー」を食べるシステムをつくりあげたということになる。太陽の光エネルギーをつかって海中のクロロフィルが光合成をして、そこに植物たちが繁茂して、その養分をつかって全生物が生きまくること、これが非平衡開放系の生命系をつくりあげた生物たちの最大の特色になったのである。
　しかし、このような説明は「エントロピーの矢」と「時間の矢」の関係については何も解読していない。のみならず「秩序が生まれる」ということを「情報の矢」の仕事とみなすのなら、「エントロピーの矢」と「情報の矢」はなんらかの帳合いをとって折り合いをつけているはずなのに、そのこともこのような熱力学論議からは説明できない。すなわち、「時間の矢」や「エントロピーの矢」を生命系にあてはめようとしたとたん、往々にして科学の得意なロジックの多くが立ち往生してしまうのだ。

　だから言わないこっちゃなかっただろうという気分に、ぼくはまた戻っている。時間を時間だけとりあげて議論するのは、もう無理なのである。それだけではなく、時間をｔや-ｔといった時間だけで成立させているかぎり、エントロピーも情報もいったんは自立して考えざるをえなくなって、仮にそれらの関係をまぜこぜにしたくとも、それをすることができなくなってしまうのだ。
　せめて「時空」を単位に思考をすすめるか、「時間の非対称性」を最初からロジックに入れておくか、それとも時間をひとつの単位にしないで、メタ時間や時間子や派生時間子といったことを勘定に入れておくようにするべきなのだ。熱力学と時間のことを説明しようとすると、ぼくはいつもこういう気分になってしまうのだ。