禁断の市場

Ｑ　 明けましておめでとうございます。

Ａ　 はい、おめでとう。今年もよろしく、本賀新年（笑）。

Ｑ　 ２０１０年の正月はどうでしたか。

Ａ　 ちょっと風邪気味でね、でも、なんとか気分は上々だった。

Ｑ　 どんなことをされていたんですか。

Ａ　 テレビはラグビーと箱根駅伝と「日本と朝鮮半島２０００年」アンコール放映だけ、外出は丸善の松丸本舗と松屋の「川喜田半泥子展」だけ。あとは本のちらちら読みだね。

Ｑ　 ちらちらはどんな本ですか。

Ａ　 ギリースの確率論、ルーマンのシステム論、森村進のリバタリアニズム論、金子勝の反経済学、ミヒャエル・エンデの寓話あたりを好きに読んでいた。そう、そう、ちょっとした発掘もあった。

Ｑ　 何ですか。

Ａ　 歳末の買い出しついでに寄った東急文化村のＮＡＤｉＦＦで見つけた一冊でね。買ってすぐにドゥマゴのオープンカフェで熱い珈琲と煙草をやりながらさっと半分くらい眺めたあと、おとといその続きを読んだもので、ハンス・アビングの『金と芸術』（グラムブックス）という本です。アーティストはなぜ貧乏なのかということを突き止めている（笑）。経済社会と芸術社会の剥離をいろいろ暴いていて、ちょっとおもしろい。

Ｑ　 あいかわらず変わった本も読んでるんですね。それで、松岡さんの今年はどんなふうになりそうですか。

Ａ　 そうだねえ、よほどラディカルか、よほど意外か、よほどパンクかという１年かな。「根底で洒落てみる」ということ。これがぼくの年頭の所感というやつかな。

Ｑ　 根底で洒落る？

Ａ　 うん、根底と洒落を同時に語るというのは、容易ではないよね。容易ではないけれど、やっておきたい。小林秀雄（９９２夜）のようにとか、エミール・シオラン（２３夜）のようにということではなく、ひたすら無棒玄月ふうに。「春泥に不空羂索、大笑い」というかな。はっはっは。

Ｑ　 なんだかよくわかりませんが（笑）、まあ、いいです。松岡さんのことだから、何か魂胆があるんでしょう。で、千夜千冊もそうなっていくんですか。

Ａ　 いや千夜千冊は、それじゃない。そういうラディカル・パンクな思想芸風をお見せするというわけにはいかない。やっぱり連環篇は「リスク」とはいったい何かということを問うことから始めたわけだから、まだしばらくは、リスクをむやみに避けるようになってしまった現在の社会や生き方や経済思想に、あれこれ文句をつけていかなくちゃね。何もかもに賞味期限をつけすぎだよ。そのツケ、どうするんだろうね。

Ｑ　 日本がですか。

Ａ　 うん、まずは日本がね。ぼくはね、世の中も人生も哲学も、リスキーであるほうがずっといいと思っている。そもそもリスキーでない仏教や趣味やスポーツなんて、あるわけがないよね。仕事だって恋愛だってむろんリスキーでしょう。だから冒険心も恋心も募るわけだ。最近は“草食男子”という輩（やから）がふえているらしいけれど、これはたんにリスクを負いたくない、失敗したくないということだね。

Ｑ　 リスクだらけなのに、ですね。

Ａ　 むろん歴史はもともとリスクに満ちている。いまでも世の中、そのままです。太古からね。ところが近現代史というものは、総じてはリスク回避とリスク分散ばかりをめざしてきた。とくに保険社会と学校社会と企業社会が、そうしすぎてきたよね。これはね、さしずめ「組織化された無責任」というもので、その波及たるや甚だしい。そんなことばかりしたので、みんな冒険しなくなった。危ないものには手を出さない。社会や会社そのものが草食男子化している。

Ｑ　 みんなが決めた危ないものだけ、みんなで叩く。ノリピーとか喫煙者とか天下り官僚とか。

Ａ　 そう、そう、その通り。おかげで案の定、いまやすべからくリスク後遺症に病んでいる。だからしばらくはそのオーバーエクステンションなお膳立てにいちゃもんをつけておく必要があるんだね。

Ｑ　 ネオリベ、金融工学、とりわけデリバティブ、それと悪しきグローバリゼーションですか。

Ａ　 いやいや、そういう“まるごと批判”だけですましていてはダメだね。実は金融工学だって、初期にめざしたリスクとリターンの方程式は、悪くはなかったんです。それがなかったら市場なんておもしろくもなんともなかった。とくにオプションがね。そのことについては別の日においおい説明するけれど、それより問題はリスクの回避と分散がそのままリターンに直結すると考えたそのロジックのほうが、度しがたい病巣をもっていると言うべきだね。

Ｑ　 じゃあ、金融工学は途中からおかしくなっていったわけですか。

Ａ　 金融工学や金融機関よりも、もっとリスク後遺症のかたまりになってしまったのは、アメリカやイギリスや日本という“国家”のほうだろうね。民営化したほうが市場の自由裁量がはたらき、それゆえリターンが多いとみなして、リスクを「民」（みん）に押し付けたわけだ。国交省の前原さんがとりくんでいる日本航空の破綻もそういう例でしょう。
　そんなことばかりしたから、国家にとって何がリスクなのか、何を不確実なものとみなすのか、「おおもと」のほうがわからなくなってしまったんだね。普天間基地をどこに移転するのか、ＣＯ２排出権をどこで決着つけるのか、このままではリスクの計算にはまっていくばかりだ。こんなことじゃ、多様なオプションの狭間で立ち往生するだけだろうね。

Ｑ　 はい。そこまではわかります。となると、新年最初の千夜千冊は、国家とリスクについての本ということですか。

Ａ　 ああ、なるほど。それもいいんだけど、それはもうちょっとあとにまわそうかと思っている。今日はねベノワ・マンデルブロをとりあげようかと思っています。

Ｑ　 マンデルブロって、あのフラクタル幾何学の？

Ａ　 うん。

Ｑ　 それって、リスク論とかマネー資本主義に関係あるんですか。

Ａ　 それがあるんだな。マンデルブロは６０年代はずうっと物価変動や金融市場の調査研究をしていたんだね。その成果が重なって７０年代になってフラクタル幾何学を“発見”する。ぼくが１３３１夜でタレブの『ブラック・スワン』（ダイヤモンド社）をとりあけだのは、もちろん読んでくれたよね？

Ｑ　 はい、読みました。

Ａ　 あそこに、タレブが「この本をベノワ・マンデルブロに捧ぐ」としてあったことはおぼえている？

Ｑ　 えっ、ええ、まあ、なんとなく。

Ａ　 だったら見当がつきそうなものだけれど、『ブラック・スワン』って何を書いていたかというと、ランダムウォーク理論と正規分布で金融市場を席巻しようとしたことに大いなる過ちがあって、そこを「マンデルブロ的ランダムネス」に、また「フラクタル分布」にしてみなさいと言っているわけだ。

Ｑ　 は、はい、そうでした。

Ａ　 だからマンデルブロはね、もともと「トポロジー経済学」みたいなものからフラクタル幾何学を出してきたんです。その後もマンデルブロはずっとフラクタル・ファイナンス理論のようなことを研究していますよ。

Ｑ　 すみません、ちょっと見当がつかなかったです。

Ａ　 そう？　トポロジーの基本は「トポス＋ロギア」でしょう。これは何かというと、位置（トポス）がもつ情報をなにがしかの次元に変じてみせる学（ロギア）がトポロジーだということだよね。

Ｑ　 はい、ええ、まあ。

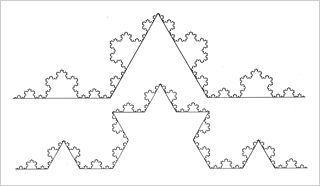
Ａ　 そのトポロジカルな次元の目で見ると、牛蒡も小豆も、キュウリもミカンも、五線譜も書棚も、次元を変換していけば似たものになっていく。コーヒーカップとドーナツは同じ次元になる。トポロジーって、そういう「位相の意味」の変化に着目した幾何学だから、そこに市場の位置（トポス）として、物価変動の値やリスクの値が入ってきたっておかしくないわけです。次元をどういうふうにするかだけどね。正確にいえば次元数。

コッホ曲線のフラクタル次元（２つの整数の間の非整数の値を取る次元）
上の基準となる折れ線を3分の1の長さに縮小し４つ連ねると
下の複雑な折れ線を描くことができる
基準となる線を縮めて測定する作業を繰り返すと各段階で線の長さは4/3倍づつ長くなる
フラクタル次元はこの変化の比率（対数の比）によって定義される

Ｑ　 その、次元をどうこうするというのは、どういうことですか。

Ａ　 次元というのは、物体や空間や時間にこびりついているものではないんだね。次元は測定の方法にかかわっている。見方にかかわっているものなんです。次元は「見方のサイエンス」なんだ。

Ｑ　 はあ。

Ａ　 たとえばここに、手のひらに入るほどの毛糸のかたまりがあるとして、毛糸に着目すれば１次元の紐になり、数百メートル先から見れば０次元の点になりますね。虫メガネや顕微鏡で見れば、毛糸そのものにもケバケバとモヤモヤがついていてかなり複雑な構造が浮上するよね。つまり、次元でものを見るというのは、スケーリングによって対象や現象を変えながら見ていくということです。
　ただし長らくのあいだ、こうした次元の異なるスケーリングを一貫した方法で比較検討する幾何学がなかったんです。それをやってみせたのがマンデルブロのフラクタル幾何学だった。

アルプスか月の山か
スケーリング（見方）が定まらないために間違えてしまう

マンデルブロ集合
見る場所やその倍率によって少しずつ異なる形を見せるマンデルブロ集合
驚くべき多様性と結果の複雑さが作りだされる

Ｑ　 われわれがなんとなく知っているフラクタル幾何学って、図形的な自己相似形の幾何学なんですが、それがどうして市場動向の研究から生まれてくるんですか。

Ａ　 フラクタル幾何学って、全体の様子をそれなりの割合で縮小すると部分が再現できるようになっているわけだよね。
　これはいいかえれば、拡大しても縮小しても似たような性質が見えてくるように「見方のサイエンス」を作ったということで、そこにフラクタル幾何学の特色があるってことです。だからこそ、たとえば気候モデルや河川のツリー構造や、脳波のパターンや地震のゆらぎ、あるいはウェブに流れる情報流動や画像のデータ圧縮などが、同じ目で比較できるようになった。最近のＣＧでは、これらをほぼ同じ情報圧縮のアルゴリズムで再現できるよね。

Ｑ　 ええ、マンデルブロの本には樹木の枝とかカリフラワーの房とか、それから河川の分岐構造、リアス式の海岸線とかを解析した図がいろいろ載ってますね。

コンピュータによって描かれたフラクタル図形（左）
肺の気管支の複雑な分岐構造（右）

航空写真の海岸線（下）とランダムなフラクタル曲線（上）

Ａ　 電話のノイズとか、引きちぎられた金属の断面とかもね。
　フラクタル幾何学の次元をつかった見方では、こういうものはほぼ同じものに見えてくるわけだ。”相似律”ですよ。でも、マンデルブロはそういうものを“発見”する前は、株価指数や為替相場の変動を河川の分岐構造と同じように、トポロジー変換することをやっていたんです。

Ｑ　 なるほど、そこまではとりあえず了解しました。で、今夜はそのマンデルブロのどういう本をとりあげるんですか。

Ａ　 これだね。

Ｑ　 えっ、『禁断の市場』？　凄いタイトルですね。これがマンデルブロ？

Ａ　 まあ、邦訳タイトルだからセンセーショナルにしたんだろう。原タイトルは“The (Mis) Behavior of Markets”というもので、（Mis）が付いているのがいいね。サブタイトルは“A Fractal View of Risk, Ruin, and Reward”となっている。日本語版のほうは「フラクタルでみるリスクとリターン」。

Ｑ　 はあ、本当にフラクタルとリスクが結びついているんだ。で、これはマンデルブロが書いたんですか。

Ａ　 マンデルブロが語った内容を、「ウォールストリート・ジャーナル」ヨーロッパ版のリチャード・ハドソンがまとめたものなんだけれど、一貫して「私は」というふうに、マンデルブロが書いたかっこうをとっている。
　このハドソンという人物は「ウォールストリート・ジャーナル」で２５年も編集記者を務めていたらしく、そのうち６年間は編集主幹だったそうだから、金融市場については玄人はだしで、だからフラクタルきわまりないリスク論を、マンデルブロが自分が歩んできた道を辿りながら語りあげたような構成がつくれたんだろうね。よくできているよ。初期の金融工学の入門書にもなっている。

Ｑ　 帯には、「ランダムウォーク理論からは、バブルの発生と崩壊は予想できない」とか「フラクタル幾何学によって解き明かされた金融市場の本当の姿」ってありますね。
　ふーん、そうか、フラクタルと金融市場ってもともと関係あるんだ。ランダムウォーク理論を批判したわけですからね。フラクタル幾何学って「たまたま」の科学の延長なんですね。

Ａ　 例の、日本では広中平祐が監訳した『フラクタル幾何学』って大著がありますね。あの原タイトルは知ってる？

Ｑ　 いえ、知りません。

Ａ　 １９７７年のものなんだけれど、あれは“FRACTALS : Form, Chance and Dimension”というもので、「形と偶然と次元」というふうになっている。これをね、たとえば「かたかたち・たまたままたまた・みかたかた」なんてするとおもしろい。

Ｑ　 まあ、松岡さん、おしゃれですね（笑）。形と次元で「たまたま」を相手にした幾何学ということですか。で、その『禁断の市場』という本は、それが市場のなかのリスクとリターンの関係から見えてきたということを書いてるんですか。なるほど、ちょっとおもしろそうですね。

Ａ　 反応が遅いねえ。『ブラック・スワン』をちゃんと読んでくれなかった報いだな。ま、いいや。この本については翻訳者にも注目するといい。監訳者の高安秀樹という人は東北大学の情報科学研究科にいて、いまはソニーのコンピュータサイエンス研究所にいるんだけれど、おそらく本書の翻訳者として最適な人物でしょう。『フラクタル』（朝倉書店）という著書がある一方で、『経済物理学の発見』（光文社新書）といった著書もあって、市場にそひむエコノフィジックスの研究に精を出している。

Ｑ　 経済物理学なんて学問があるんですか。

Ａ　 ごく最近のものだけれど、ちょっと注目されている。これもマンデルブロのおかげだね。高安さんは１９８８年にイェール大学に在籍していたころは、マンデルブロの研究室に１年ほど入りびたっていたらしい。かつてぼくはジョン・ブリックスとデヴィッド・ピートの『鏡の伝説』（ダイヤモンド社）という本にいたく感心したことがあるんだけれど、いま思い出すと、高安さんはその翻訳者の一人だった。
   『経済物理学の発見』も読んでみるといいよ。この手の本では日本では唯一だ。本格的なものとしては、プショーとポッターが書いた『金融リスクの理論』（朝倉書店）もあります。それからぐっとわかりやすいものに、謎の人物として知る人ぞ知るの、犬走文彦の『反経済学講座』（新潮社）というものもある。これもいい。

Ｑ　 わかりました。ぜひそのあたりも読んでみます。で、マンデルブロはどういうふうに金融市場の研究など始めたんですか。だいたいどういう人でしたっけ。

Ａ　 マンデルブロはユダヤ系のポーランド難民なんです。１９２４年にワルシャワで生まれた。ポーランドはやがてナチス・ヒトラーの侵攻を受けるよね。その戦火のなか、マンデルブロの一家はパリに脱出する。で、そのパリにも戦火が及ぶと、少年マンデルブロは郊外に送られて、馬の世話や工具の修理をする。一家がリヨンの支援者に匿われていたとき、やっと学校で勉学に励むんだけれど、そのときすでに算数問題を図形的に解くことにめざめたらしい。というふうに、この本で自伝的に語っているね。

Ｑ　 自伝みたいになっているんですか。

Ａ　 半分、自伝調だね。で、戦後になると、１９４５年にフランスで最も有名な大学のひとつのエコール・ノルマル・シュペリエールに入ったようなんだけれど、なぜかここを２日間でやめて、エコール・ポリテクニークに入りなおしている。ちょっと変わってるね。何かに染まりたくない気質があったのか、最初の大学には本能的に自分に合わないリスクを感じたかしたのかねえ。その後はアメリカに渡ってＣＡＬＴＥＣ（カリフォルニア工科大学）に入ると、さらにＭＩＴへ、それからプリンストン高等研究所へというふうに移っている。

Ｑ　 どんどん移る。ノーマッドなんですね。

Ａ　 ユダヤ系の難民だから、やっぱりディアスポラの感覚が血の中にあったのかもしれない。

Ｑ　 たしかミルトン・フリードマン（１３３８夜）もジョージ・ソロス（１３３２夜）もそうでしたね。

Ａ　 ところがプリンストンまで行ったんだから、それで学者になったのかというと、やっぱりそうではなくて、一般企業の研究所に入っている。それがヨークタウン・ハイツのＩＢＭのワトソン研究所なんだね。ワトソン研究所のことはぼくも行ったことがないので知らないんだけど、以前、北大の田中譲さんからその自由な研究風土を瑞々しく説明されたことがある。まだＩＢＭが世界で一番元気だったころの話です。
   おそらくマンデルブロにとっては、これがよかったんでしょう。最初は大型コンピュータの通信エラーの発生頻度の統計解析やデータ解析に従事しているんだけど、そのうち１９６０年代に入ると、研究所の所長から依頼されて株式市場の価格変動の解析にとりくんだ。これに夢中になるんだな。

Ｑ　 ３０代半ばですよね。マンデルブロは何に夢中になったんでしょうか。株が好きだったんですか。

Ａ　 いや、そうじゃないだろうな。研究所がどこかから委託調査を依頼されたんだろうね。マンデルブロが担当したのは綿花の動きです。それよりなにより、まずは世界一の大型コンピュータを動かすのが気にいったんだろうね。でも、たんなる数値の追っかけではない。所得の分布と綿花の市場価格の変位分布の関係を比較調査研究したりしている。この本の説明によると、乱流状態にある流体のエネルギー散逸量の変動と金融市場におけるボラティリティ（価格の変位の絶対値）の変位の類似性を研究しているね。
   というわけで、マンデルブロの最初の論文は１９６２年の経済学の論文なんです。ぼくも本書を読むまで知らなかった。『ある投機的な市場価格の変動』というものだ。

大気の乱流状態における風速変動のシミュレーション（上）
長期間の株式市場のボラティリティの変動を示したグラフ（下）

Ｑ　 じゃあ、金融工学のハシリみたいなことに着手していたということですか。

Ａ　 リスクとリターンの関係を見るわけだから、似たような領域の研究をしていたわけだけれど、いわゆる金融工学じゃなかった。それこそフラクタル・ファイナンスという見方をしていた。いや、むしろ金融市場の変化をトポロジカルに幾何学しているうちにフラクタル次元に気がついたといったほうがいいのかな。

Ｑ　 マンデルブロはシカゴ学派とはまったく関係がなかったんですね。

Ａ　 うん、異端もいいところだろうね。ただそのへんのことは、ちょっと前後関係を含めて説明しておいたほうがいいかもれない。とくに金融工学の流れとの関係をね。金融工学についてはどのくらい知ってるの？

Ｑ　 われわれがその名を知ったときは、もうネオリベ・グローバリゼーションやマネー資本主義の悪しき先兵として批判されてましたから、ほとんど接点はありません。

Ａ　 ああ、そうなんだ。ま、いいだろう。詳しいことはさておいて、ごくごく簡単にいうと、今日に至る金融工学（financial engineering）を支えてきたのは、やたらに出来のいい数理モデルってやつなんだよ。それも主として３つの数理モデルによっている。

Ｑ　 難しい話になりそうだなあ。どういうものですか。

Ａ　 発表順にいうと、「モダンポートフォリオ理論」（ＭＰＴ）、「資本資産価格モデル」（ＣＡＰＭ）、「ブラック＝ショールズの公式」という３つかな。ビジネススクールに入ってＭＢＡ（経営学修士）をめざす連中は、まずはこの３つの徹底学習から入る。そういうものです。
    ＭＰＴから説明すると、マンデルブロが６０年代初期にワトソン研究所で市場の調査研究にとりくんでいたころ、すでにハリー・マーコビッツという男がシカゴ大学時代に提唱した「平均・分散モデル」というものが話題になっていたんだね。これは、いまではいろいろな手直しと発展を受けたうえでのＭＰＴ（モダンポートフォリオ理論）とよばれているもので、資産の分散投資によって平均的収益を一定に保ちながら、かつリスクを軽減する方針を理論化したというモデルです。初めてリスク分散をモデル化したポートフォリオだった。

Ｑ　 凄いんですか。

Ａ　 有名な話だけれど、シカゴ大学でマーコヴィッツの論文が審査されたときは、ミルトン・フリードマン（１３３８夜）が「これは経済学でもないし、数学でもない」と言ったらしい。意地悪で言ったんじゃなくて、統計とか確率に強くなかったフリードマンにはそうとしか思えなかったんだろうね。
   でも証券業界では、MPTのポートフォリオはまたたくまに広がった。なにしろ、どんな銘柄でもリスクとリターンをあらわす二つの数字、つまり売却時に期待できる利益の平均と分散の数字を使いさえすれば、基本的な投資計画が計算できるというものだったからね。

Ｑ　 それが金融工学の出発点になるんですか。

Ａ　 いや、それはこのあとだね。マーコヴィッツのＭＰＴには、正規分布のベル型カーブに頼っていたこと、ポートフォリオを作成するのに膨大な計算が必要になっていたことなどの、いくつかの難点があって、そのへんを改良してからだ。最初にＭＰＴを新たに組み替えたのは、当時ＣＡＬＴＥＣの学生だったウィリアム・シャープという青年です。

Ｑ　 学生ですか。凄いなあ。

Ａ　 シャープは、そのころシカゴ大学からランド・コーポレーションに移っていたマーコヴィッツ先生を突然に訪れて、あれこれのヒントをもらうと、たちどころに数式を仕上げた。これがのちのちまで使われる「資本資産評価モデル」（Capital Asset Pricing Model）というもので、略してＣＡＰＭというものだ。キャップ・エムと読みます。すぐに圧倒的な支持を得た。株式の適性価格の見当がつくだけでなく、企業が事業計画を出したときの評価に使えたんです。
   でも、ＭＰＴとＣＡＰＭだけではまだ金融工学の”三種の神器”は揃わない。そこへ「ブラック＝ショールズの公式」が颯爽と登場して、金融工学はここから本格化していくわけです。

Ｑ　 「ブラック＝ショールズの公式」は名前だけは知ってます。MBAにとっての”魔法の杖”みたいなものですよね。

Ａ　 オプションについての対応モデルだね。

Ｑ　 オプション？

Ａ　 あのね、１９７３年というと何を思うかな。ベトナム終戦、オイル・ショック、ブレトン・ウッズ体制の崩壊、変動相場制のスタートなど、その後の時代を決定的に画期するさまざまな出来事が前後しておこった年だよね。実は金融市場のなかでも、この年に新たなことがおこっていたんです。この年の４月２６日、シカゴ・オプション取引所（ＣＢＯＥ）が設立された。

Ｑ　 それも画期的だったんですか。

Ａ　 オプション（option）というのは、将来の一定期間のなかで約束した金額で商品を売ったり買ったりする「権利」のことだよね。買う権利がコールオプションとなり、売る権利がプットオプションになる。これが自由に取引できるようになった。
   オプションを購入するにはプレミアムとよばれるコストを支払う必要があるんだけれど、オプションをうまく利用することで原資産の価格変動リスクをヘッジできる。ここまではいいかな。それで、ＣＢＯＥが開設された日、ゼロックス社の株式を３カ月以内に１株１６０ドルで１００株買う権利のオプションが、３９件売り出されたんだね。オプション・プレミアムは１株につき５ドル５０セント。この日、ニューヨーク証券取引所ではゼロックス株の終値は１４９ドルだったので、ＣＢＯＥで１６０ドルのコールオプションに手を出した投資客は、きっとゼロックス株の値上がりを期待したということだよね。
   その期待が図に当たって、もし３カ月以内に１株１７０ドルまで上がったならば、客はオプションの権利を行使して１株１６０ドルで買い入れ、即座に１７０ドルで売れば、プレミアムの５ドル５０セントを差し引いた利益が手に入るということになる。逆に値下がりしたまま期限切れになれば、オプション・プレミアムは戻ってこない。
   このＣＢＯＥのオプション取引があっというまに人気をとったんです。それまでも投資市場では先物（さきもの）とか先渡（さきわたし）といったオプション取引はあったんだけれど、ごく小規模な店頭取引のみで、ブローカーがいて互いに電話やテレックスで取引をしているようなものだったんだね。価格も公表されないし、手数料も高くついていた。
　それが手早くなっただけでなく、ニューヨーク取引所では１株１４９ドルで実際に株を購入しなければならないのに、ＣＢＯＥでは「権利」だけで投資ができるようになったんだから、これは金融市場の歴史に新しい方向を開いちゃったわけだ。だって、仮に値上がりがおこらなかったとしても、損失はプレミアムの５ドル５０セントだけですむんだからね。みんな手を出した。

Ｑ　 いやあ、わかるような、わからないような話です。

Ａ　 そう？　まあ取引のメカニズムはともかくとして、オプションについては、もっと現代思想こそがとりあげるべきだねえ。今日の資本主義社会やグローバリゼーションを議論するなら、オプションの思想を省いているのはよくない。

Ｑ　 そうなんですか。

Ａ　 うん、そうだ。オプションの思想に注目したほうがいい。

Ｑ　 そんなことを現代思想で言う人はいなかったですよね。

Ａ　 うん、きっとぼくが最初かもしれないね。だいたい、optical（視覚的）、optimism（楽天主義）、optimum（最適性）、option（選択権）といったＯＰＴ語類は、かなり要注意な関係にあるんだよ。オプティカルに見ようとすることがオプションなんです。

Ｑ　 あっ、高山宏さんふうですね（笑）。

Ａ　 連塾（２００９年１２月１９日）に来たんだな。

Ｑ　 もちろん伺いました。興奮、興奮でしたね。

Ａ　 まあ、オプションについては語源的なものだけでなくて、人間の意思決定の問題としても重要だし、社会やシステムがどのように選択肢をつくっていくかということでも大事だし、なにより近い将来のことを勘定にいれた規範って何なのかということが大事だよね。だってオプションって、フィードフォワードとフィードバックの両方でできていくんだからね。
   それはともかくとして、このＣＢＯＥのオプション取引をしてみると、ひとつ、よくわからない問題があったんです。

Ｑ　 はい、何でしょうか。

Ａ　 オプション・プレミアムの価格はどうして決まるのか、そこがわからない。価格はもちろん他の商品と同じように、売り手と買い手のあいだで決まっていくのだけれど、なぜその価格になるのかという、その妥当性がどうしても読めない。みんな、そこを知りたくなっていったわけです。
　オプション商品はそもそもが時間を先送りして、その先送りのなかに不確実な要素を生かしておいて、これをリスクヘッジしようというのだから、先が読めなければ勝ち目がまったくわからない。ただ、この価格決定の解法については、経済学の大御所ポール・サミェルソンも手を上げていたらしい。

Ｑ　 それくらい難問だった？

Ａ　 まあ、そういうことだね。ところが、これをやすやすと解法に導いた連中がいた。その一人がフィッシャー・ブラックで、一人はマイロン・ショールズ、もう一人はロバート・マートン。これが金融工学の確立を決定づける、かの「ブラック＝ショールズの公式」というものになる。”魔法の杖”だね。

Ｑ　 松岡さんは「ブラック＝ショールズの公式」がわかるんですか。

Ａ　 はっはっは、わかるわけないよ（笑）。超難しいし、わかりたくもない。でもね、フィッシャー・ブラックについては、ペリー・メーリングが７年をかけて書き上げたという『金融工学者フィッシャー・ブラック』（日経ＢＰ社）という本を読んでみて、うーん、これは天才的だなと感じたね。ハーバード大学で物理学と応用数学を修め、アーサー・Ｄ・リトルに入っていた男で、ふつうなら、オプション取引では権利行使日の株価を予想することこそ重要であると思うだろうに、ブラックはその予想と関係なく利益予測が計算できることを発想するんだね。
   オプション権の行使日と行使価格と銘柄のボラティリティさえ代入すればいいはずの公式がありうると、そう直観したわけですよ。つまり、トレーダーがすでにもっている数値だけで計算できる公式がありうるはずだと発想したんです。ブラックはさっき言ったＣＡＰＭだけを前提に、これを一気に考えたらしい。

Ｑ　 天才はどの分野にもいますからね。金融部門にいたって当然です。

Ａ　 ニヒルだな。というよりただの反発だな（笑）。でも、一人だけの作業じゃない。公式まで導いたのは、シカゴ大学で経済学を修めてそのころＭＩＴに来ていたマイロン・ショールズと、コロンビア大学やＣＡＬＴＥＣで工学や応用数学を専攻したのちにＭＩＴに来ていたロバート・マートンとの共同作業のようなんだけれど、その公式の発表が、なんと１９７３年の５月。ＣＢＯＥが開設された翌月なんだね。
   テキサス・インスツルメント社は、さっそく新発売の電卓でブラック＝ショールズ公式が計算できるようになっていると宣伝し、メリルリンチ社はＣＡＰＭ自体の組織的業務化にとりくんで、ブラック＝ショールズの公式を操れる職員を育てあげることにしたらしい。

Ｑ　 松岡さん、マンデルブロはどうなったんですか。

Ａ　 あっ、そうだね。いささか金融工学の黎明期の話をしすぎたけれど、いやいや、もっと詳しくも紹介したいのだけれど、それは別の機会に譲るとしてね、だいたいはこういうような時期に、ベノワ・マンデルブロもまた市場にひそむ法則の発見やリスクとリターンの関係にひそむ法則の発見を求めて、フラクタル・ファイナンスの着想に向かっていたということです。でも、ポートフォリオ・モデルやＣＡＰＭやブラック＝ショールズの公式には、何かおかしいところがあると感じていた。

Ｑ　 どのへんがおかしいと感じていたんでしょうか。

Ａ　 さっきから言っているし、『ブラック・スワン』のときも書いたけれど、モダンポートフォリオ理論以降の、金融市場の“神技”みたいに認知されていった公式群には、二つの典型的な特徴をもっていたんだね。
　ひとつは、昨日の変動は今日の変動に影響を及ぼさないというランダムウォーク理論にもとづいているということです。これは確率微分方程式になっている。ランダムウォークの何が問題かということは、ムロディナウの『たまたま』（１３３０夜）に書いたから、わかるよね。
　で、もうひとつは、偶然がどんどん積み重なっていっても、それがかなりの量になればそこには正規分布（ベル・カーブ）であらわされるものがあるはずだという見方です。
   ランダムウォークと正規分布。これがあやしい正体だった。タレブは『ブラック・スワン』で、「ベル・カーブ、この壮大な知的詐欺」とか、「まやかしの不確実性」とか書いていたよね。マンデルブロもそこに気がついた。正規分布ではなくてベキ分布になるんではないかということに気がついていった。

ブラック＝ショールズの公式に基づいてオプションの市場価格を推定したグラフ
データにもとづいて導出した価格変動リスク（ボラティリティ）が補正されるも
その僅かな計算の誤差がオプションの世界では何百万ドルの損失につながる

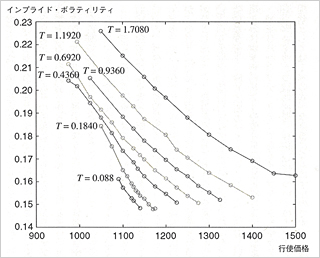
Ｑ　 ベキ分布？　ああ、やっぱりわからない。これはわれわれにはお手上げですよ。

Ａ　 そうかな。まあ、あと少しでやめるから、もうちょっと。マンデルブロはどうしてベキ分布やフラクタル分布の重要性に気がついたかというところだけでも聞きなさい。

Ｑ　 はい、わかりました。お正月ですからお手柔らかに。

Ａ　 さきほどのべたように、６０年代に入ってマンデルブロがＩＢＭフェローとしてのワトソン研究所で取り組んでいたのは、綿花の価格変動の調査と研究だったよね。ただ、いくら研究しても、そこに法則はあらわれない。
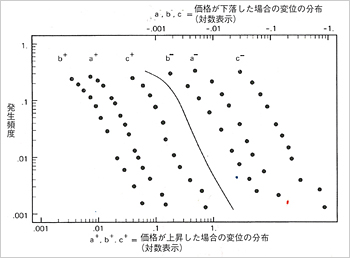
　とりあえずマンデルブロは過去１００年の綿花価格の変動のデータを集め、これをさまざまなコモディティ（商品）の動きと比較した。それまでの確率論や統計学の数学も検討してみた。以来、数年の曲折をへて、何かが欠けていたと思っていたものが、あるとき意外な方向からやってきたようなんだね。セレンディピティでしょう（１３０４夜）。それも、まったく別々の方角から、３つやってきたらしい。それがベキ乗則、個人所得（貧富）の分布、安定分布の理論というものだった。マンデルブロでなければつなげられないような３つだね。

ベキ乗則を対数グラフ用紙に描いた図
直線の傾きがベキの指数を表している
直線は1、正方形のタイルは2、立方体の体積は3の傾きをとる
フラクタル図形になると直線の傾きは整数を取らず、半端な値をとる

所得の分布曲線
パレートによる人間社会の富の分布グラフ
縦軸を上るほど所得が高くなり、横軸は所得層の人の数を表している
所得の分布曲線はベル曲線に反して非対称を示す

グラフ用紙に描いた綿花価格の分布図
左は価格が上昇した場合の変位を右は価格が下落した場合の変位を表している
abcの異なった時間スケールからなるいずれのケースも似たような傾きを示し
綿花価格のフラクタルな価格変動（L-安定分布に起因するベキ乗則）が見て取れる

Ｑ　 はい、どうぞ先を。

Ａ　 ふてくされているな（笑）。このセレンディピティには感動してもらいたかったんだけどね。まあ、いいか。もう少し聞きなさい。ベキ乗則のヒントは、ジョルジュ・ジップの『人間の行動と最小努力の法則』と、社会における均衡を見いだす循環理論を説いたヴィルヒリオ・パレート（1848～1923）のパレート分布からやってきたようなんだ。

Ｑ　 はい。

Ａ　 ジップはね、「統計人間生態学」という独特の分野をつくりあげた人物で、社会のさまざまな現象にベキ乗則がありうることを提示したんです。
　たとえば文章のなかに出てくる単語の頻度数ってあるね。そこで、使われた頻度の高い単語から頻度順にランクをつけて、これをランクと頻度のベキ分布の座標軸に並べると、そこに何かのグラフが見えてくるでしょう。頻度の多い単語から少ない単語に向かってなだらかな曲線になるだろうというのが、ふつうの予想だよね。
　ところが驚くべきことに、上位ランクの単語はランクが下がるにつれて急激に落ちていくのにくらべ、ランク下位の単語はとてもゆっくり減少していたんだね。そういうプロット分布になった。
   これが「ジップの法則」とよばれるもので、いわば「博学度の特色」をあらわしているようなもんだ。博学とは非対称な知識の使い方だったということだねえ。

Ｑ　 どういうことでしょう？

Ａ　 だって知識をもった奴って、何かの傾向をもっているわけだ。それが専門語にもそうじゃない言葉にもあらわれている。得意な用語は上位にかたまって、その分野が過ぎると急激に落ちる。まあ、専門家ってそんなものでしょう。ところがふだん使う言葉のほうはぐちゃぐちゃとなだらかな曲線になる。こういうことがベキ乗則を使うと見えてきた。そういうことだね。で、マンデルブロはこれをフラクタル・スケーリングに組み立てなおしていった。

Ｑ　 それ、知識人批判にも使えますね。

Ａ　 調べてみたら？　で、パレート分布のほうは説明するまでもないだろうけれど、社会のなかの富の数値（所得と人数）をベキ乗にプロットしたもので、ジップの法則と同様に正規分布にはならずに、やはり非対称のベキ分布になる。
   もうひとつマンデルブロが注目したのは、パウル・レヴィの確率論です。これは「安定分布の理論」とよばれているもので、安定というのは対象や現象を転がしたり揺らしたりぶつけたりしても、その基本的な性質が変わらないことをいう。
   マンデルブロは以上のセレンディップにやってきたベキ乗則、貧富分布、安定分布の３つを組み合わせて、そこにさらに時間スケールの変動を入れ、綿花の株価の動向にあてはめてみたんですね。時間スケールを入れるというのは、そのモデルの出方を早送りしても見え方が変わらないことをさすわけだ。
   こうして、これらの手続きをしたうえで、そこに出現してきたのが価格変動の最初のフラクタル性だったということです。わかった？

フラクタル市場の立方体
ランダムな価格のブラウン運動を表したチャート（左）
気まぐれに伸び縮みさせるトレーディング時間の変動（中央）
時間の伸び縮みとランダムな価格変動を混合したマルチフラクタル価格チャート（右）

金融マルチフラクタルのパノラマ
線分を折れ線に置き換える簡単なモデルを用い
様々な価格変動のチャートをシミュレートするスケーリングマルチモデル

Ｑ　 すみません。わかりませんでした。

Ａ　 そうか。このぶんじゃ、今年はどうも前途多難だな（笑）。まあ、そのうち見えてくるよ。ベキ分布についても、いつか詳しく説明しよう。それをやるのがぼくの千夜千冊のお役目なんだから。では、今年もよろしく。